Fulgence Bienvenüe

Auteur/autrice : admin0

  • Activité N°3: Puissance solaire reçue

    Inclianaison des faisceaux lumineux et surface éclairée

    https://www.geogebra.org/classic/YyRwjmx7

    Inclinaison des faisceaux lumineux en fonction de la latitude et de la période de l’année

    https://www.geogebra.org/classic/PuSKjRbu

  • 2e appli

    TUTO ÉLÈVES — DUPLIQUER LE PROJET ET MODIFIER POUR AFFICHER LE DÉBIT D’EAU

    Objectif

    Repartir d’un projet qui marche déjà, puis changer :

    • l’URL
    • la clé à afficher

    1) Dupliquer le projet

    1. Dans MIT App Inventor : Projects
    2. Cliquer sur My Projects
    3. Trouver votre projet MotAleatoire (ou le nom de votre projet “Mot”)
    4. Cliquer sur More actions (les 3 points / menu)
    5. Choisir Copy project
    6. Nommer la copie : DebitEau

    ✅ Vous avez maintenant le même projet, mais pour le débit.

    2) Modifier l’écran (Designer)

    Dans Designer :

    A) Modifier le bouton

    • Cliquer sur BtnMot
    • Changer son texte en : Lire le débit
    • (Optionnel) Renommer le bouton : BtnDebit
      👉 Si vous renommez, il faudra retrouver les blocs correspondants.

    B) Modifier le label

    • Cliquer sur LabelMot
    • Changer son texte en : --
    • (Optionnel) Renommer : LabelDebit

    👉 Pour aller vite : ne renommez pas les composants, changez juste le texte.

    3) Modifier l’URL de l’API (Blocks)

    Aller dans Blocks.

    Dans :

    when Screen1.Initialize

    Remplacer l’URL :

    ✅ Ancienne :
    https://trouve-mot.fr/api/random

    ✅ Nouvelle :
    https://proxy-automate.latelier22.fr/api.php

    4) Modifier CE QU’ON AFFICHE (Blocks)

    Dans le projet “Mot”, on affichait :

    • clé "name" (dans l’objet)

    Ici, on veut afficher :

    • clé "debit_eau_l_h" (directement dans data)

    Dans when Web1.GotText → dans le then

    Vous gardez la ligne qui décode le JSON :

    ✅ Garder :

    • set global data to JsonTextDecodeWithDictionaries(responseContent)

    Ensuite, vous changez la partie “mot”.

    A) Supprimer les blocs inutiles

    Supprimez :

    • la ligne set global obj to select list item ...
    • la ligne set global mot to get value for key "name" ...
    • la ligne set LabelMot.Text to get global mot

    B) Remplacer par UNE SEULE ligne

    Ajoutez :

    set LabelMot.Text to

    • join
      • get value for key "debit_eau_l_h" in dictionary (get global data) or if not found "--"
      • " L/h"

    ✅ Ça affichera par exemple : 56.88208 L/h

    5) Vérification rapide

    Cliquez sur le bouton :

    • si tout va bien : un nombre apparaît + L/h
    • sinon : le label affiche “Erreur API”

    6) (Optionnel) Arrondir à 2 décimales (plus propre)

    Remplacez l’affichage par :

    • join (format as decimal debit 2) " L/h"

    (Je te donne la version exacte en blocs si tu veux l’ajouter.)

    Résumé ultra simple

    1. Copier le projet
    2. Changer l’URL
    3. Supprimer “obj” et “name”
    4. Afficher "debit_eau_l_h" + " L/h"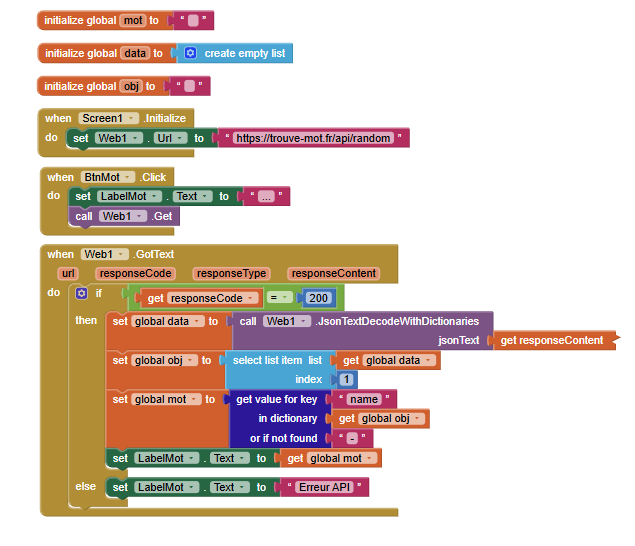

  • Ma première appli mobile

    TUTO MIT APP INVENTOR — “Mot au hasard”

    Objectif

    Quand on clique sur Nouveau mot, l’appli appelle l’API :

    https://trouve-mot.fr/api/random

    et affiche le champ name (ex : “flèche”) dans un Label.

    1) DESIGNER (écran de gauche)

    A. Créer les composants

    Glisser-déposer sur l’écran :

    1. Button
      • Rename : BtnMot
      • Text : Nouveau mot
    2. Label
      • Rename : LabelMot
      • Text : Appuie sur le bouton
      • FontSize : 28 (ou 30)
    3. Web (non visible)
      • Rename : Web1

    2) BLOCKS (écran de droite)

    A. Créer 3 variables globales

    Menu Variables → prendre initialize global name to et renommer :

    1. initialize global mot to ""
    2. initialize global data to create empty list
      • (bloc Lists → create empty list)
    3. initialize global obj to ""

    3) Mettre l’adresse de l’API au démarrage

    Menu Screen1 → bloc :

    when Screen1.Initialize do

    À l’intérieur :

    • set Web1.Url to "https://trouve-mot.fr/api/random"

    ✅ Important : on ne met PAS Web1.Get ici.

    4) Quand on clique sur le bouton : appeler l’API

    Menu BtnMot → bloc :

    when BtnMot.Click do

    À l’intérieur :

    1. set LabelMot.Text to "..." (chargement)
    2. call Web1.Get

    5) Quand l’API répond : extraire le mot

    Menu Web1 → bloc :

    when Web1.GotText (url, responseCode, responseType, responseContent) do

    A. Vérifier que c’est OK

    Mettre :

    if get responseCode = 200 then

    ⚠️ 200 doit être un nombre (bloc bleu), pas “200” en texte.

    B. Dans le THEN, mettre ces 4 lignes

    1) Décoder le JSON

    Menu Web1 :

    • set global data to
      • call Web1.JsonTextDecodeWithDictionaries
        • get responseContent

    ✅ Le JSON reçu est une liste (ça commence par [)

    2) Prendre le 1er élément de la liste

    Menu Lists :

    • set global obj to
      • select list item
        • list = get global data
        • index = 1

    3) Récupérer la clé « name »

    Menu Dictionaries :

    • set global mot to
      • get value for key
        • key = "name"
        • in dictionary = get global obj
        • or if not found = ""

    4) Afficher dans le label

    • set LabelMot.Text to get global mot

    C. Dans le ELSE (si erreur)

    • set LabelMot.Text to "Erreur API"

    ✅ Résultat attendu

    Quand on clique sur Nouveau mot :

    • Le label passe à ... (chargement)
    • Puis affiche un mot (ex : flèche)

  • thème_n°3_-_chapitre_1_-_activité_2_-_a_la_surface_du_soleil.

    thème_n°3_-_chapitre_1_-_activité_3_-_puissance_solaireTélécharger

    Doc réponse

    CORRIGÉ

    🌍 Problématique

    Pourquoi observe-t-on des températures différentes entre l’équateur et les pôles ?

    👉 La cause principale est la variation de la puissance solaire reçue en fonction de la latitude.

    1️⃣ Influence de la latitude sur la température

    Les trois villes étudiées sont :

    • Dakar (~14° N)
    • Copenhague (~55° N)
    • Nuuk (~64° N)

    🔎 Températures maximales (lecture graphique)

    • Dakar : ≈ 28 °C
    • Copenhague : ≈ 17 °C
    • Nuuk : ≈ 7 °C

    ✅ Conclusion :
    Plus la latitude augmente (on se rapproche des pôles), plus la température maximale diminue.

    2️⃣ Températures moyennes annuelles

    📍 Dakar

    Moyenne calculée à partir du tableau (page 1) :Tˉ≈25°C\bar{T} \approx 25°CTˉ≈25°C

    📍 Copenhague

    Moyenne graphique ≈ 8 °C

    📍 Nuuk

    Moyenne graphique ≈ –2 °C

    ✅ Conclusion :
    Plus la latitude est élevée, plus la température moyenne annuelle est faible.

    3️⃣ Rôle de l’angle des rayons solaires (Doc.2 et Doc.3)

    À l’équinoxe de printemps :

    • À l’équateur : rayons verticaux
    • Aux latitudes élevées : rayons plus inclinés

    Quand les rayons sont inclinés :

    • L’énergie se répartit sur une surface plus grande
    • Donc la puissance reçue par m² diminue

    4️⃣ Formule de la puissance solaire reçue

    La puissance reçue par m² dépend de l’angle d’incidence :PR=PE×cos⁡(α)P_R = P_E \times \cos(\alpha)PR​=PE​×cos(α)

    avec :

    • PE=1000 W.m−2P_E = 1000 \, W.m^{-2}PE​=1000W.m−2
    • α\alphaα = angle entre le rayon lumineux et la verticale

    5️⃣ Calcul de la puissance reçue à l’équinoxe

    Angles donnés (Doc.3) :

    • Dakar (14°)

    PR=1000×cos⁡(14°)≈970 W.m−2P_R = 1000 \times \cos(14°) \approx 970 \, W.m^{-2}PR​=1000×cos(14°)≈970W.m−2

    • Copenhague (55°)

    PR=1000×cos⁡(55°)≈570 W.m−2P_R = 1000 \times \cos(55°) \approx 570 \, W.m^{-2}PR​=1000×cos(55°)≈570W.m−2

    • Nuuk (64°)

    PR=1000×cos⁡(64°)≈440 W.m−2P_R = 1000 \times \cos(64°) \approx 440 \, W.m^{-2}PR​=1000×cos(64°)≈440W.m−2

    🎯 Conclusion générale

    ✔ Plus la latitude augmente :
    → Les rayons solaires sont plus inclinés
    → L’énergie est répartie sur une surface plus grande
    → La puissance reçue par m² diminue
    → La température moyenne diminue

    🌞 Conclusion scientifique finale

    Les différences de température entre l’équateur et les pôles s’expliquent principalement par la variation de l’angle d’incidence des rayons solaires avec la latitude, ce qui modifie la puissance solaire reçue par mètre carré.

  • Révisions collége

    Série d’exercices – Diagnostic / Révisions

    Objectifs : fractions (\(+\), \(−\), \(×\), \(÷\)), signes, calcul littéral (réduire, distributivité, double distributivité), factoriser.

    Nom : ____________________    Date : ____ / ____ / ______    Durée : 1h

    1) Nombres relatifs

    Série 1 : Calculs simples

    1. \((+4) + (-7)\)
    2. \((-5) – (+3)\)
    3. \(-(-8) + (-2)\)

    Série 2 : Avec parenthèses

    1. \(-(-3 – 4)\)
    2. \((-6) – (-9) + (-2)\)
    3. \(-[(-5) + 7]\)

    Série 3 : Multiplications

    1. \((-4)\times(-3)\)
    2. \((-7)\times 5\)
    3. \(-2\times(-6)\)

    2) Réduire (calcul littéral simple)

    1. \(3x + 5x\)
    2. \(7x – 2x\)
    3. \(-4x + 9x\)
    4. \(2x + 3 + 5x – 4\)
    5. \(-6x + 2 – 3x + 8\)
    6. \(9x – 4 + 2 – x\)
    7. \(3x^2 + 5x^2\)
    8. \(7x^2 – 2x^2 + x^2\)
    9. \(-4x^2 + 9x^2 – x^2\)

    3) Distributivité simple

    1. \(3(x + 4)\)
    2. \(-2(x – 5)\)
    3. \(5(2x + 3)\)
    4. \(-4(3x – 2)\)
    5. \(x(2x – 7)\)
    6. \(-3x(4 – x)\)

    4) Double distributivité (développer et réduire)

    1. \((x + 3)(x + 2)\)
    2. \((2x – 5)(x + 4)\)
    3. \((3x – 2)(2x + 1)\)
    4. \((x – 7)(x – 3)\)
    5. \((-x + 4)(2x – 3)\)
    6. \((5x + 1)(-2x + 3)\)

    5) Fractions – Addition / Soustraction

    1. \(\frac{1}{3} + \frac{1}{6}\)
    2. \(\frac{5}{8} – \frac{1}{4}\)
    3. \(\frac{7}{10} + \frac{3}{5}\)
    4. \(\frac{2}{7} – \frac{3}{14}\)
    5. \(\frac{9}{4} – 1\)
    6. \(2 + \frac{3}{5}\)

    6) Fractions – Multiplication

    1. \(\frac{2}{3}\times\frac{5}{4}\)
    2. \(\frac{7}{9}\times\frac{3}{5}\)
    3. \(\frac{4}{11}\times\frac{22}{3}\)
    4. \(\frac{5}{6}\times 3\)
    5. \(\frac{8}{15}\times\frac{9}{4}\)
    6. \(\frac{12}{7}\times\frac{14}{3}\)

    7) Fractions – Division

    1. \(\frac{3}{4}\div\frac{2}{5}\)
    2. \(\frac{7}{8}\div\frac{14}{3}\)
    3. \(\frac{9}{10}\div\frac{3}{5}\)
    4. \(2\div\frac{5}{6}\)
    5. \(\frac{11}{3}\div\frac{22}{9}\)
    6. \(\frac{4}{7}\div 2\)

    8) Factoriser (simple)

    Consigne : mettre le facteur commun en évidence.

    1. \(4x + 8\)
    2. \(6x^2 + 9x\)
    3. \(12x – 3x^2\)
    4. \(10x^2 – 5x\)
    5. \(14x + 21\)
    6. \(8x^2 – 16x\)

    9) Factoriser (facteur commun) – niveau “complexe”

    Consigne : repérer le facteur commun puis factoriser.

    1. \((2x + 1)(x + 3) + (x + 3)(4x – 2)\)
    2. \(3x(2x – 5) + 7(2x – 5)\)
    3. \((x – 4)(3x + 2) – (x – 4)(x – 1)\)

    10) Mélange complet (niveau contrôle)

    1. \(2(x + 3) – 3(2x – 1)\)
    2. \(\frac{1}{2}(x + 4) – \frac{3}{4}x\)
    3. \((2x – 1)(x + 2) + (x + 2)(3x + 4)\)
    4. \(\frac{3}{5} + \frac{2}{3}\times\frac{9}{4}\)
    5. \((x + 1)^2\)
    6. \((x – 3)^2\)

    Auto-évaluation : Fractions ☐ / Signes ☐ / Développer ☐ / Factoriser ☐

    Remarque : _________________________________________________

  • Recherche des métiers

    Recherche (libellé)
    ROME parent (optionnel)
    Classification
    Emploi cadre
    —
    Page: 1 / 1

  • France travail API métiers

  • HABITAT: Chapitre 1 : Energie et puissance électrique

    HABITAT

    Chapitre 1 — Énergie et puissance électrique

    1ère STI2D • Sciences Physiques

    Notions / contenus

    • Gestion de l’énergie dans l’habitat
    • Énergie, puissance, conservation, rendement

    Capacités attendues

    • Citer différentes formes d’énergie présentes dans l’habitat
    • Exploiter la relation puissance–énergie
    • Donner des ordres de grandeur des puissances utilisées

    I) L’énergie \(E\)

    I-1 Définition

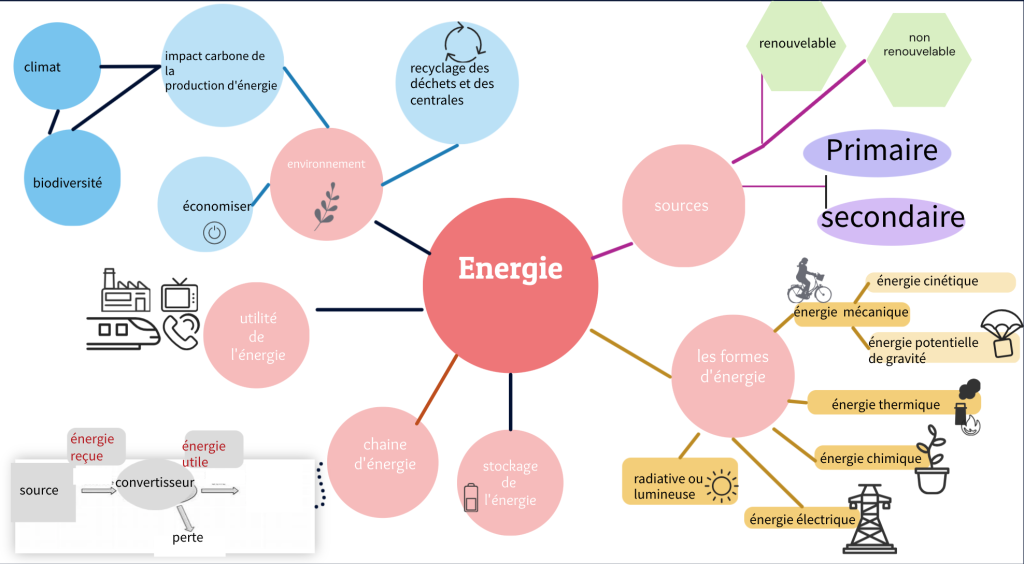
    L’énergie est la capacité d’un système à produire un travail (mouvement), de la lumière ou de la chaleur. C’est une grandeur physique qui caractérise l’état d’un système.

    Unité légale : \(E\) et \(W\) en joule : \(J\)

    Repère : \(1\,W \cdot s = 1\,J\)

    Unités d’énergie (selon l’usage)

    Unité Équivalence (en J) Usage
    kWh (kilowattheure) \(1\,kWh = 3{,}6 \times 10^6\,J\) Énergie domestique / facturation
    tep (tonne équivalent pétrole) \(1\,tep = 4{,}2 \times 10^{10}\,J\) Économie / bilans énergétiques
    eV (électronvolt) \(1\,eV = 1{,}6 \times 10^{-19}\,J\) Physique atomique
    cal (calorie) \(1\,cal = 4{,}18\,J\) Diététique

    I-2 Différentes formes d’énergie (dans l’habitat)

    • Énergie cinétique (augmente avec la vitesse et la masse)
    • Énergie potentielle de pesanteur (augmente avec l’altitude et la masse)
    • Énergie chimique (réactifs → chaleur, etc.)
    • Énergie thermique (chauffage)
    • Énergie électrique (appareils domestiques)
    • Énergie lumineuse (lampes)
    • Nucléaire → électrique (centrales)

    II) La puissance \(P\)

    II-1 Définition

    La puissance échangée est le rapport de l’énergie échangée par la durée de l’échange :

    \[ P = \frac{E}{\Delta t} \]

    Unités : \(P\) en \(W\), \(E\) en \(J\), \(\Delta t\) en \(s\).

    Relation équivalente : \[ E = P \cdot \Delta t \]

    Dans l’habitat, l’énergie est souvent en kWh. Exemple : \(1\,kWh = 3{,}6 \times 10^6\,J\).

    Exercice 1 — Haltérophiles

    Deux haltérophiles fournissent la même énergie \(E = 2\,kJ\) en soulevant une masse \(m = 100\,kg\) sur \(2\,m\). Le premier met \(t_1=1\,s\), le second \(t_2=1{,}5\,s\). Calculer \(P_1\) et \(P_2\) puis comparer.

    Conclusion : à énergie égale, plus la durée est faible, plus la puissance est grande.

    Exercice 2 — Lave-linge

    Un lave-linge nécessite \(P = 3000\,W\) pendant \(t = 2\,h\). Calculer l’énergie consommée en \(kWh\) puis en joules. S’il est utilisé 100 fois/an et que le prix est 13 centimes par \(kWh\), calculer le coût annuel.

    II-2 Ordres de grandeur (puissance des appareils)

    AppareilPuissance typique
    Frigo150–350 W
    Lave-vaisselle≈ 1200 W
    Cafetière500–1000 W
    Hotte70–150 W
    Four à micro-ondes1000–1500 W
    Four électrique2000–2500 W
    TV90–350 W
    Éclairage10–25 W
    Lampe halogène≈ 300 W
    Console de jeux20–180 W
    Sèche-linge2500–3000 W
    Lave-linge2500–3000 W
    Fer à repasser750–1100 W
    Aspirateur650–800 W
    PC de bureau70–120 W
    Téléphone portable5–10 W
    Radio-réveil5–10 W
    Rasoir électrique8–12 W
    Chauffage d’appoint1000–2000 W
    Sèche-cheveux300–600 W
    Exercice 3 — Console

    Calculer l’énergie dépensée en \(kWh\) par an pour une console de puissance \(P = 180\,W\) utilisée 1 heure par jour.

    III) Conservation de l’énergie et rendement

    III-1 Conservation

    Énergie absorbée = énergie utile + énergie perdue :

    \[ E_a = E_u + E_p \]

    On peut aussi écrire la conservation des puissances :

    \[ P_a = P_u + P_p \]

    En général, l’énergie perdue est souvent sous forme de chaleur.

    Exercice — Bilan d’énergie

    Dessiner le schéma du bilan d’énergie pour : lampe électrique, lave-vaisselle, chaudière au fioul, ordinateur. Indiquer l’énergie reçue, l’énergie utile, l’énergie perdue et écrire l’équation de conservation.

    III-2 Rendement d’un appareil

    Le rendement est le rapport « utile / absorbé » :

    \[ r = \frac{P_u}{P_a} = \frac{E_u}{E_a} \]

    Le rendement est sans unité (rapport de grandeurs de même unité).

    Exercice — Chaudière

    Une chaudière fournit \(P_u = 100\,kW\) mais reçoit \(P_a = 108\,kW\) (pertes). 1) Donner \(P_u\), \(P_a\), \(P_p\). 2) Calculer \(r\). 

    flowchart TB
  A["Energie recue
    ELECTRIQUE"] --> B["CONVERTISSEUR
    LAMPE"]
  B --> C["Energie utile
    LUMINEUSE"]
  B --> D["Energie perdue
    THERMIQUE"]

  E["Conservation : Ea = Eu + Ep"]:::eq
  B --- E

  • Référent Sécurité Numérique (RSN)


     actions RSN

  • QCM anglais : Les pronoms

    QCM anglais: pronoms

    Chargement du QCM…